Sets#
Very briefly, a set is a collection of things (called elements) that share some property. We write sets between \('\{'\) and \('\}'\). For example, \(\{a, b, c, ..., z\}\) is the set of lowercase letters. Some more numbery examples:
And so on. If \(a\) is an element of a set \(A\), we write \(a \in A\).
Set Operations#
Sometimes, sets share elements. For example, \(\mathbb{N}\) and \(\mathbb{Z}\) both contain \(0\). If \(A\) and \(B\) are sets, then \(A \cap B\) is the set of all the shared elements of \(A\) and \(B\), called the intersection. For example, \(\mathbb{Z} \cap \mathbb{Q}^+ = \{1, 2, 3, ...\} = \mathbb{N} - \{0\}\).
Intersection has a dual operation called union and written \(A \cup B\) which gives you the set of elements that are either in \(A\) or \(B\) (or possibly both). So if \(EVEN\) is the set of even integers and \(ODD\) is the set of odd integers, then \(EVEN \cup ODD = \mathbb{Z}\).
Finally, if all the elements of one set are also in another set, we write \(A \subseteq B\) and say \(A\) is a subset of \(B\). If there’s some \(a \in A\) that’s not in \(B\), then \(A \not\subseteq B\). For example, \(\mathbb{N} \subseteq \mathbb{Z}\) but \(\mathbb{Z} \not\subseteq \mathbb{Q}^+\). Try and work out whether its true that \(A \cap B \subseteq A \subseteq A \cup B\) (or vice-versa).
Click me for answer
Yes. \(A \cap B\) is the set of elements that are in both in \(A\) and \(B\), so they are definitely all in \(A\). Similarly, \(A \cup B\) is the set of elements that are in \(A\) or \(B\), so it contains all of \(A\).
A trick for remembering the difference between \(\cap\) and \(\cup\) is that \(\cap\) sort of looks like an N and you can sort of think of the elements of \(A \cap B\) as the elements of “A aNd B”, meanwhile \(\cup\) sort of looks like a U and you can sort of read \(A \cup B\) as “A Uor B”…
Functions#
Sets by themselves are fairly boring. Things get more interesting when we can hop between them. One way of hopping between sets is using functions. A function \(f\) from a set \(A\) to another set \(B\) (written \(f: A \to B\)) takes in an element of \(A\) and spits out an element of \(B\). Symbolically, if \(a \in A\), then \(f(a) \in B\). Crucially, a function will always spit out the same element of \(B\) for a given element \(a \in A\).
Examples:
The identity function \(id: A \to A\) does nothing: \(id(a) = a\). Turns out to play a very important role for a function that does so little.
The addition function \(+ : \mathbb{N} \times \mathbb{N} \to \mathbb{N}\) does what you would expect \(+(n, m) = n + m\). The \(\times\) symbol means the function takes in a pair of elements.
If you had a set of names, you could describe everyone’s age with the function \(age: NAMES \to \mathbb{N}\)
You can learn a lot about sets by studying the functions in and out of them. For example, if you have a function \(f: A \to B\) that maps every \(a \in A\) to a different \(b \in B\), then you know that \(A\) is bigger than \(B\) (we call this an injection). Similarly, if every \(b \in B\) is mapped to by some \(a \in A\), then you know that \(B\) is bigger than \(A\) (we call this a surjection). So if you have both of these properties, the sets are the same size! We call this a bijection. You may find this picture useful:
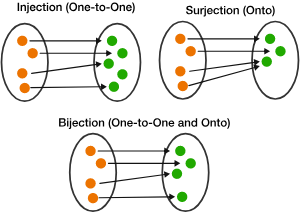
More examples:
The identity function from above is a bijection, albeit a very uninteresting one.
The straightforward function \(in: \mathbb{N} \to \mathbb{Z}\) which sends \(n \in \mathbb{N}\) to itself is injective. But it is not surjective because nothing is mapped to \(-1\).
The obvious function \(\mathbb{N} \to \{EVEN, ODD\}\) is surjective because there are even and odd numbers. But it is not injective because \(2\) and \(4\) are both mapped to \(EVEN\).
Imagine the function that maps someone’s name to their seat on a plane. This is injective because two people can’t sit on the same seat. If the plane is fully booked, then it is bjiective.
Typically, when there is a bijection we consider the sets to be basically the same and write \(A \simeq B\).